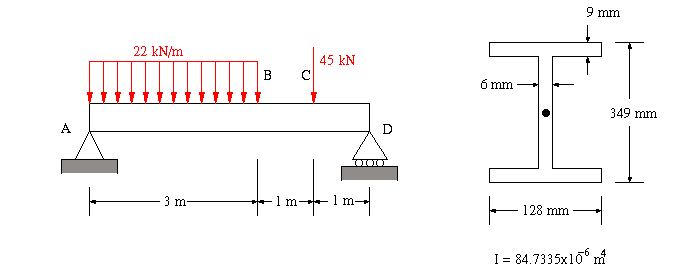
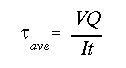
(a) To find the maximum transvere shear, the shear at each section along the beam between sections A and D must be found. This means that we need to draw the shear diagram. To do this we have to take the following steps:
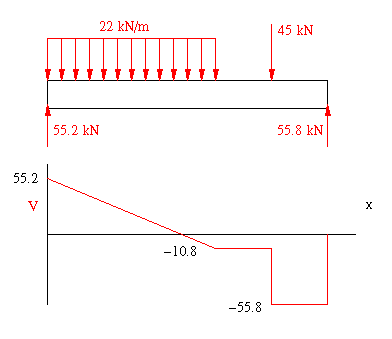
From the free body diagram, the reactions at A and D are
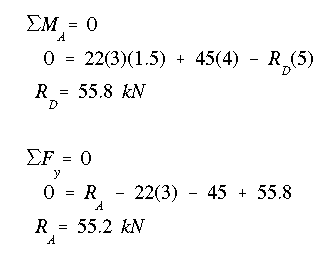
The transverse shear variation along the section with distributed force can be found by using the integral equation
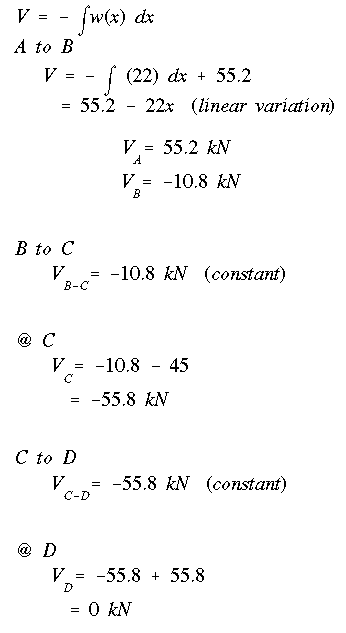
The resulting shear diagram shown below indicates that the maximum shear force is Vmax = 55.8 kN and it occurs along portion CD.
(b) For the shear flow analysis we must consider a beam section with maximum shear force. In this case any section along portion CD will satisfy this requirement. To obtain the shear flow, first draw the picture of the cross section. Since the moment of inertia about the horizontal centroidal axis (perpendicular to the direction of V) is already given, we can go directly to the moment of area (Q) calculation. Begin at the free end of the top right flange where we know the shear flow is zero, and consider a portion of length s as shown in the figure below.
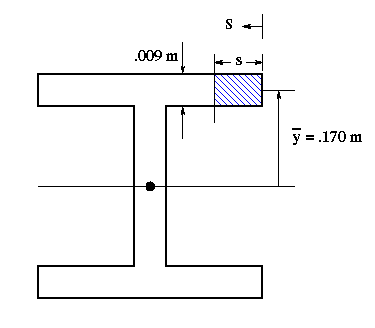
Write the equation for the shear flow in terms of the moment of area of the portion of length s.
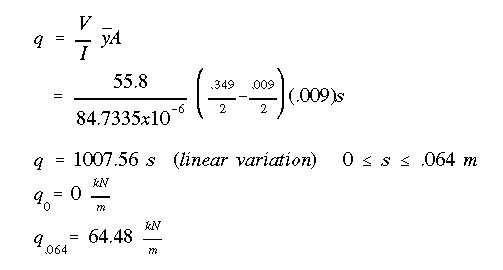
Notice that the moment of inertia is that of the entire I cross section about the horizontal centroidal axis, which is perpendicular to the direction of V.
Due to symmetry about the vertical centroidal axis, the shear flow in the top left flange will be the same as the flow in the top right (same magnitude, opposite direction). Also due to symmetry about the horizontal centroidal axis, the shear flow in bottom flanges will be the same as the ones on top (same magnitude, opposite direction).
In the web, the shear flow doesn't start from zero, like it did in the flanges. This is because the starting point of the web is a junction and not a free end. The starting shear flow for the web is shown in the figure below.
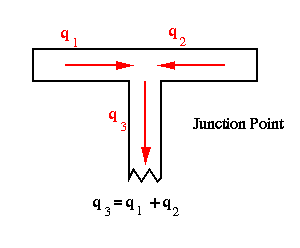
Using the fluid flow analogy the flow coming into the web-flange junction from flanges must leave the junction through the web.
To determine the shear flow variation along the web, isolate a section of length w along the web as shown in the figure below.
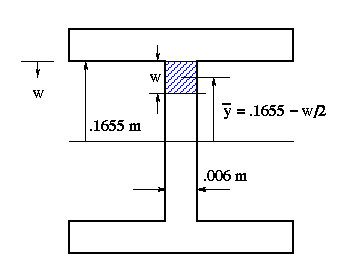
Write the shear flow equation by writing the starting value which is 128.96 kN/m, and adding to it the contribution of the web. V/I ratio stays the same (as it should), and all that remains to be calculated is the moment of area of length w along the web.
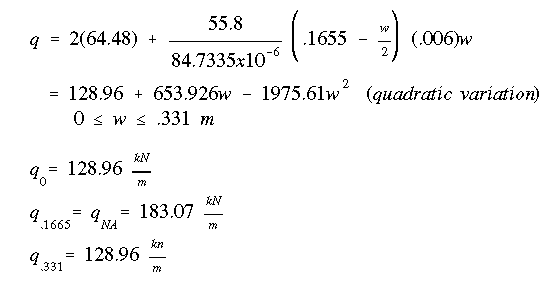
The complete shear flow diagram is shown below. The shear force in the web is found by calculating the area under the q diagram. This gives a value of 54.626 kN which represents approximately 98% of the total shear force which is 55.8 kN. The rest of it (not shown), as explained before, will be carried by the top and bottom flanges.
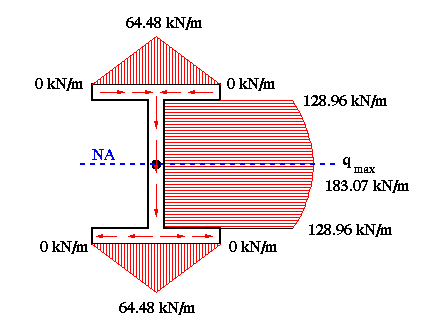
(c) Since this is a doubly symmetric cross section, the shear center is located at the intersection of the axes of symmetry which is the centroid.
(d) The maximum shear stress will occur at the point on the cross section where the ratio (q/t) is maximum. In this problem that point is located on the neutral axis.
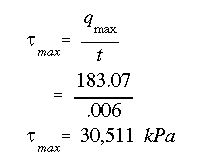
In summary, the maximum shear stress in the flange is 6.829 MPa and occurs at the intersection of the flange and the web (i.e., s = 61 mm). The minimum shear stress in the web is 21.493 MPa and the maximum shear stress is 30.511 MPa.
To Next Example
To Index Page of
Transverse Shear Loading of Open Sections
To Section III.4