NOTE:In this problem the applied transverse shear force passes through the centroid of the cross section, and not its shear center.

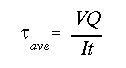
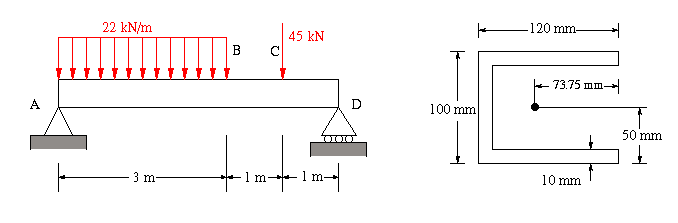
(a) To find the maximum transvere shear, the shear at each section along the beam between sections A and D must be found. This means that we need to draw the shear diagram. To do this we have to take the following steps:
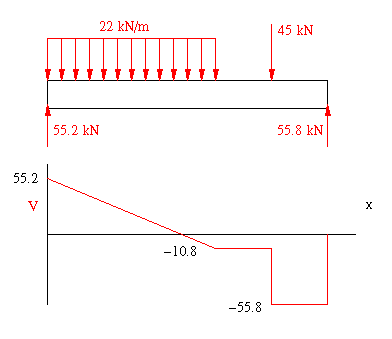
From the free body diagram, the reactions at A and D are
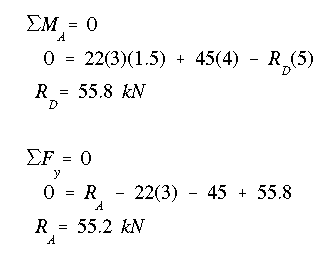
The transverse shear can be found by using mechanics of materials
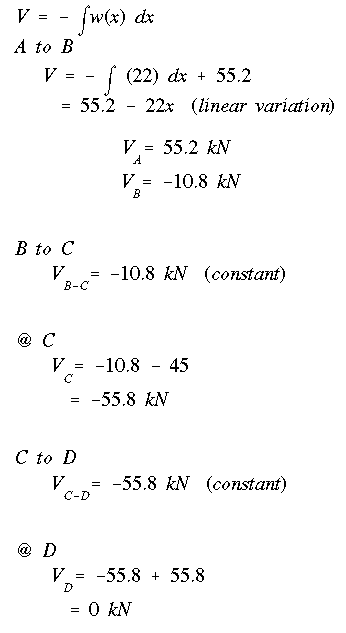
The resulting shear diagram shown below indicates that the maximum shear force is Vmax = 55.8 kN and it occurs along portion CD. Notice once again that the diagram is exactly the same as those found in the previous two example problems as the loads and boundary conditions have not changes.
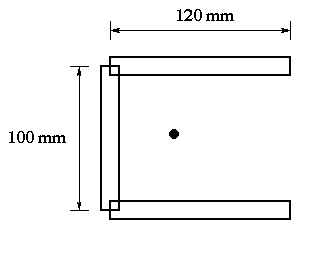
(b) For the shear flow analysis we need to have the moment of inertia about the centroidal axis perpendicular to the shear force, in this case the horizontal centroidal axis. The dimensions of the cross section are measured to the middle of each adjacent member for simplicity. Hence, the cross section can be treated as
The moment of inertia is found as
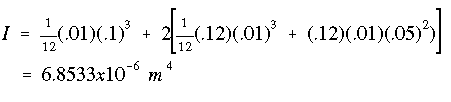
Notice that in this problem the applied lateral load does not pass through the shear center. This means that as a result of this loading, the beam will twist while bending. The principle of superposition allows us to break this problem into two parts. In the first part we will determine the shear stress due to V through the shear center, and in the second part we will determine the shear stress due to accompanying torque as was explained earlier. For the shear flow due to V passing through the shear center, we start at the free end of the top right flange by isolating a portion of length s along the flange, same as in previous examples.
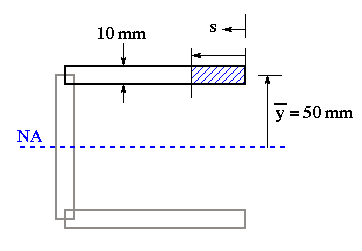
Write the equation for the moment of area of the isolated section, and put it in the shear flow equation as given below.
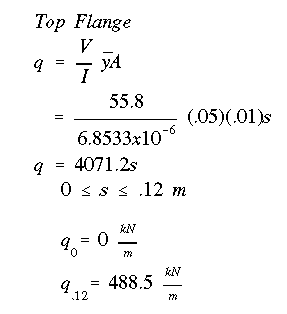
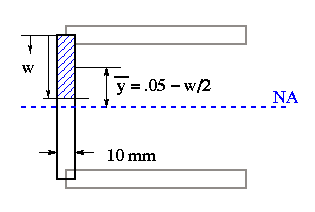
For the web start from the web-flange junction and write the shear flow equation considering the moment of area of w portion along the web.

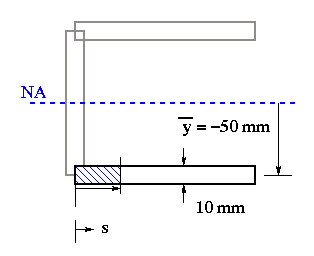
The bottom flange will have the same shear flow as the top flange due to horizontal centroidal symmetry of the cross section.
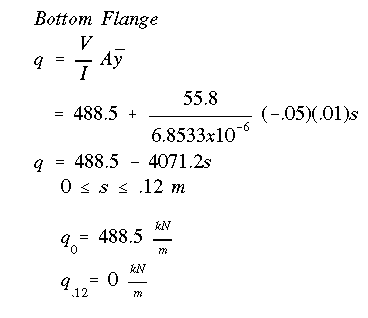
NOTE: always check your final value of q to make sure that at the free end you get zero. The shear flow diagram shown is only due to V through the shear center and does not represent the final or true shear flow variation. However, this is the variation we need in order to find the location of shear center.
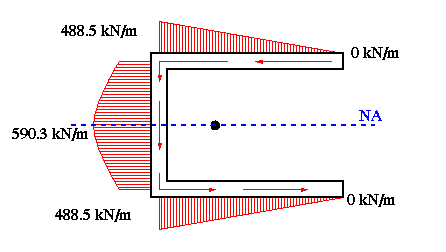
(c) Because of symmetry about the horizontal centroidal axis, the shear center must be located on that axis. Therefore, its 'y' coordinate is known. The 'x' coordinate of shear center can be determined by summing moments about the centroid. First, we need to find the force in each flange and the web. The force along each member is just the area under the shear flow curve.
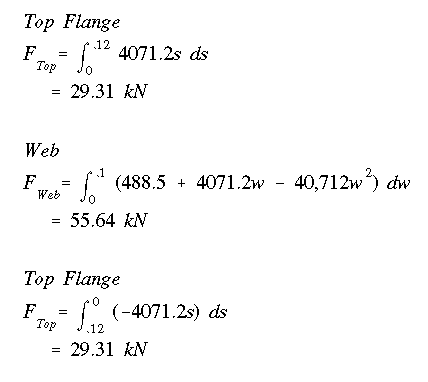
The force in the flange is the area of the triangle (the height and length would be 488.5 and .12). But as long as the equations are available, it's easier to just integrate.
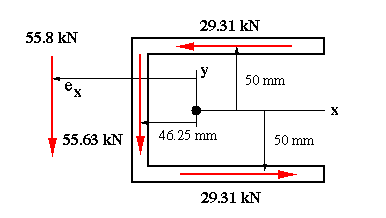
Always calculate the summation of vertical and horizontal forces, and check them against the resultant force. With only a vertical force acting on the section, the sum of horizontal forces should add up to zero, as they do. Notice that the vertical force along the web is almost 99.7% of V with the remaining 0.3% carried by the flanges as explained before. Summing moments about the centroid gives the horizontal coordinate of the shear center. Since the answer came out positive, it means that the shear center is to the left of the web as assumed.
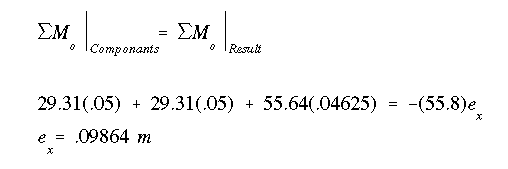
(d) The shear flow diagram shown above is only the contribution of the force through the shear center.
There is also a shear flow induced by the torque about the shear center. Knowing the location of shear center, we can now calculate the torque as shown in the figure below.
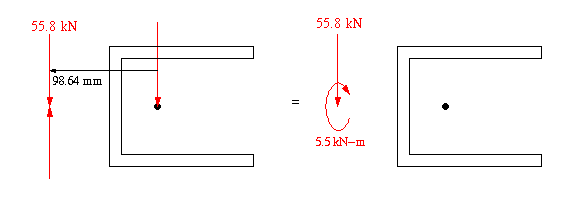
The value of torque is determined as
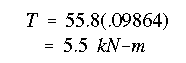
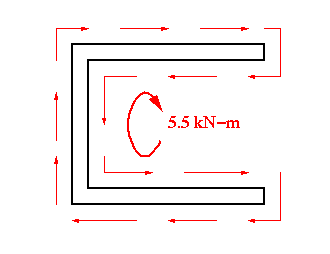
Recall from the discussion of thin-walled sections in pure torsion and the elastic membrane analogy that the shear stress contours along each member can be shown as in the figure below.
To use the equation for torque-induced maximum shear stress, we first need to calculate the a/t ratio. Since all members have the same thickness, the maximum shear stress due to torque occurs in the middle of the longest member, in this case the web.
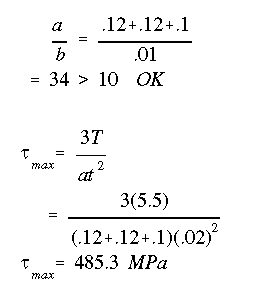
Looking at the shear stress contours, we observe that near the inside edge of the web the shear stress is downward, therefore, it would add to the one caused by the shear force through the shear center. With both components being maximum at the neutral axis, the calculation of the overall maximum shear stress would be performed as
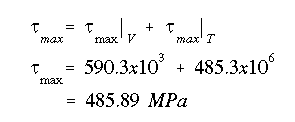
The maximum shear stress occurs at the NA, on the inside edge of the web.
 To Previous Example
To Previous Example
 To Index Page of
Transverse Shear Loading of Open Sections
To Index Page of
Transverse Shear Loading of Open Sections