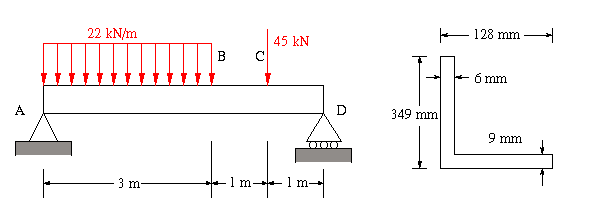

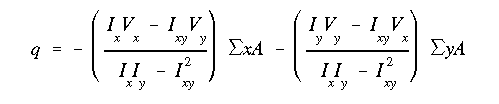
With the cross section being unsymmetric about the centroidal axes x and y, we need to calculate the product of inertia. However, first we need to know where the centroid is located. Then we can calculate the moments of inertia Ix, and Iy, and the product of inertia, Ixy. The calculations lead to the following answers:
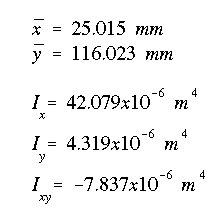
(a) To find the maximum transvere shear force, the shear at each point between A and D must be found. From the free body diagram, the reactions at A and D are
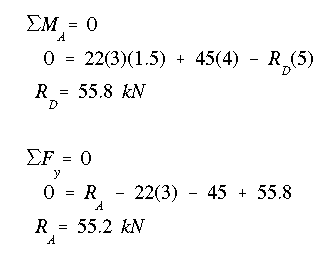
The transverse shear can be found from mechanics of materials
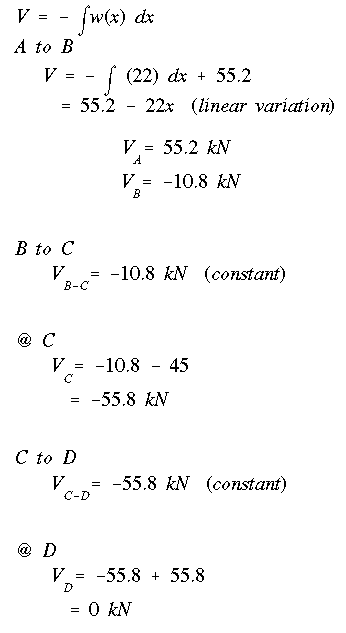
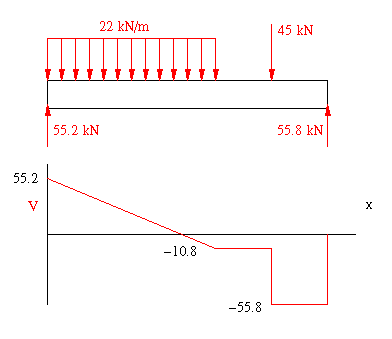
From the diagram, the maximum shear force is found to be

(b) To find the shear flow use equation A14.14. With only a vertical force acting on the section, whatever the sign, the magnitude of the shear flow will not change with the choice of sign. But to be consistent with the discussion on the sign convention, the shear force is negative along portion CD of the beam, as shown in the shear diagram.
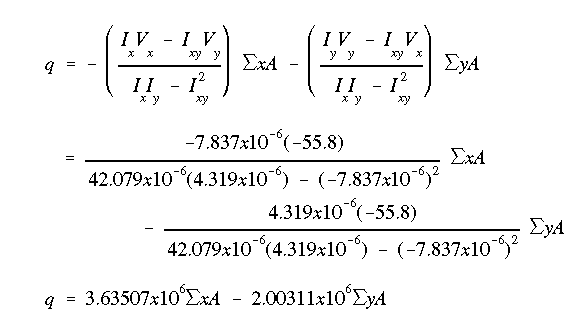
Notice that in the above equation Vx is zero, as there is no horizontal force acting on the section.
Work on one part of the general shear flow equation at a time.
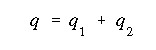

Obtain the shear flow variation by considering the summation of xA which constitutes the moment of aera Q in this case.
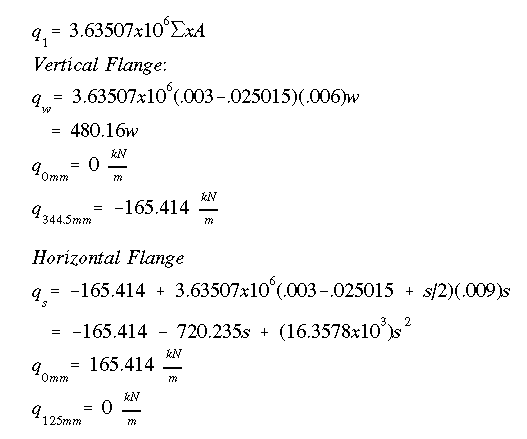
The equation for the vertical flange is linear, and it would be easy to plot. The horizontal flange would be a little harder to plot accurately as it is parabolic, we also need to obtain more information. For example, what are the roots of the shear flow equation (corresponding to a zero shear flow, which indicates a change in shear flow direction), and where is the slope of the shear curve zero (corresponding to the location of maximum shear flow along the horizontal flange).
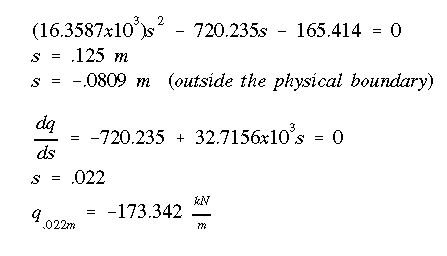
With all the necessary information determined, the shear flow distribution corresponding to part 1 of the general shear flow equation can be plotted as shown below.
Notice that the shear flow never took a zero value, except at the free ends, hence no change in sign (i.e., direction) was observed.
For this part we need to calculate the moment of area due to summation of yA.
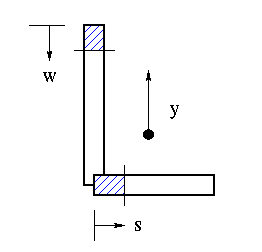
With the picture shown above, the moment of area can be calculated and put into the part 2 of the general shear flow equation as shown below.
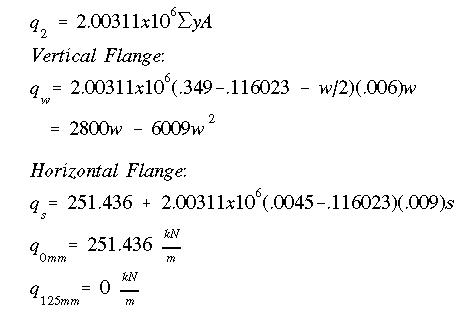
With the flow variation along the vertical flange being parabolic this time, we need to examine the equation along the vertical flange to see if shear flow goes to zero anywhere along its length.
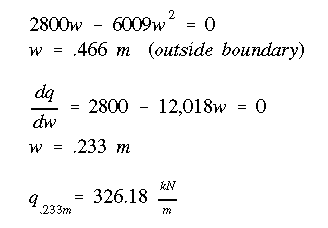
The shear flow from part 2 is shown below.
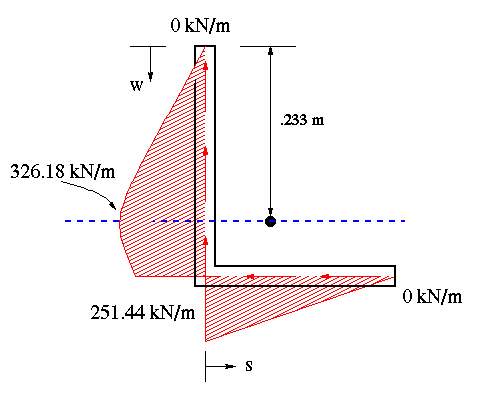
Now, combine the two parts together by adding (algebraically) the shear flow components along each flange as.

Vertical Flange
Check to see if there is a change in direction of shear flow along this flange.
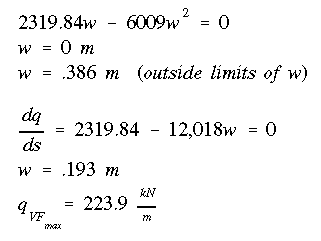
Horizontal Flange
Check to see if there is a change in direction of shear flow along this flange.
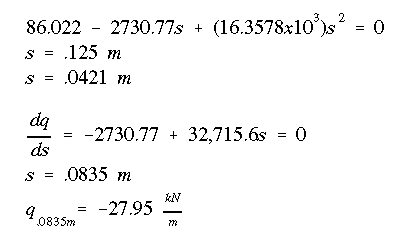
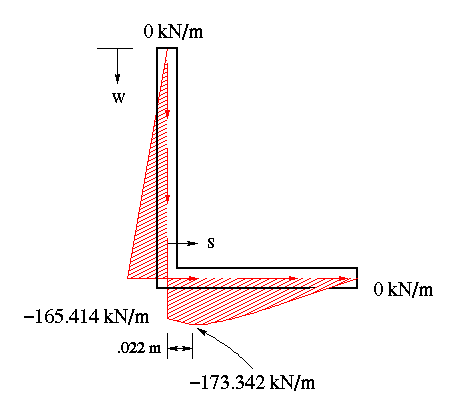
As the calculations indicate, there is infact a point along the horizontal flange where the shear flow switches direction. This is captured in the final shear flow distribution shown below.
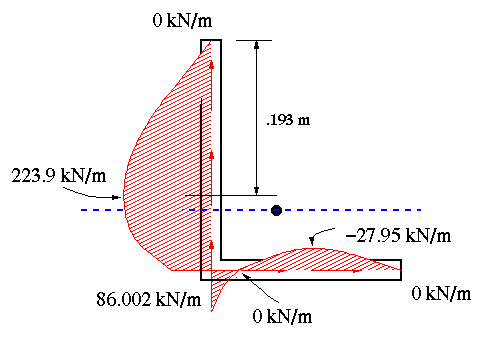
To make sure that the values found are correct. We must check the equilibrium of forces in x and y directions, individually.
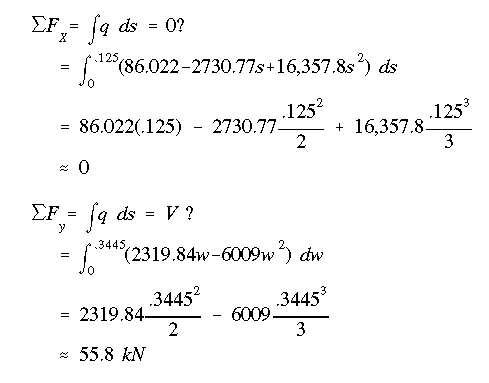
The equilibrium is satisfied. Therefore, we can presume that our analysis is correct.
(c) The 'x' component of the shear center is determined by summing the moments about an arbitrary point, here we choose point 'G' at the intersection of vertical and horizontal flanges.

With the resultant force along each flange passing through the corner of the angle section, they produce no moment about point G, therefore
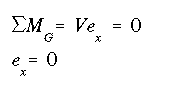
If we look at this angle section carefully, we observe that with the two flanges being identical, and separated by 90 degrees, an axis of symmetry is created along the 45 degree line between the two flanges passing through the corner. Hence, as before the shear center is located on the axis of symmetry. Notice also since this axis of symmetry was not along x or the y axes, the product of inertia Ixy did not vanish. Something to ponder upon!
 To Section III.5
To Section III.5
 To Index Page of
Transverse Shear Loading of Open Sections
To Index Page of
Transverse Shear Loading of Open Sections