(a) the shear flow distribution for a vertical transverse shear force of Vy passing through the shear center,
(b) the horizontal position of the shear center ex,
(c) the shear flow distribution for a horizontal transverse shear force of Vx passing through the shear center,
(d) the vertical position of the shear center ey.

Note: show the shear center location position relative to the centroid.

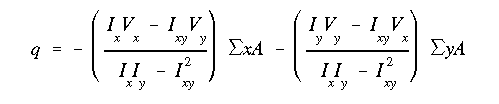
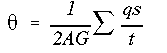
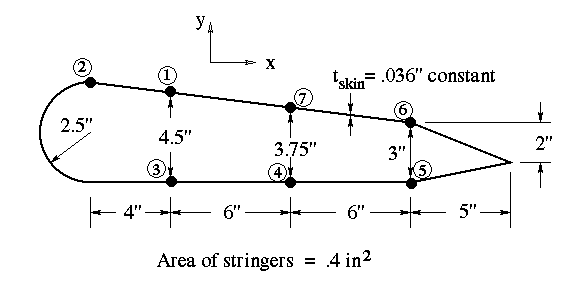
The centroid of the cross section is located at

Notice that since the stiffeners are assumed to carry the bulk of bending in skin-stringer sections, only the areas of the stiffeners are used in calculating the centroid as well as the moments of inertia.

(a) Apply a load Vy in the downward direction. We begin by removing the skin between stringers #7 and #1 so we can start from a point with a known shear flow (i.e., zero) and be able to use Eq. A14.14. With Vx = 0, equation A14.14 reduces to

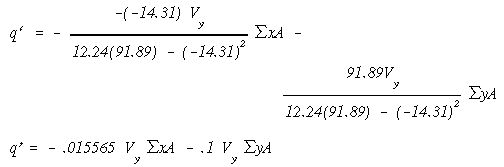
The moments of inertia are

Start at stringer #1, and work around the section.

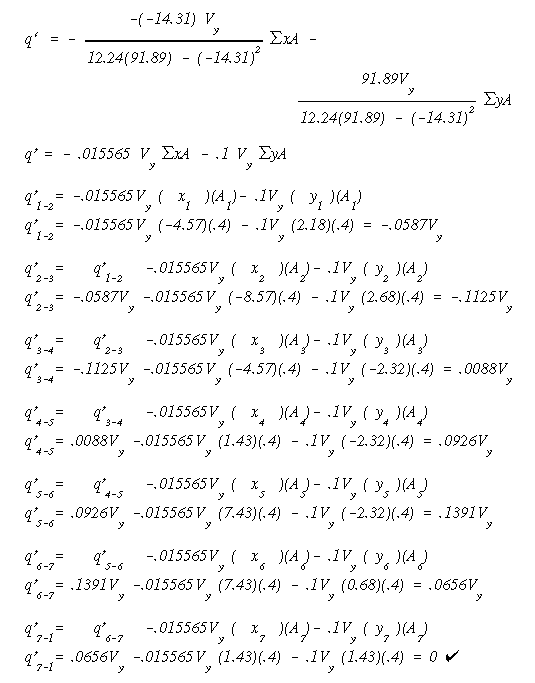
Note that the value of q' found for each web would have been the true value of shear flow if the original section was an OPEN section (i.e., with no web between stiffeners 1 & 7). This would be similar to the problems discussed previously in Chapter A14. However, in this problem we are dealing with a closed section so the q values found from Eq. A14.14 are NOT the actual shear flows, and that is why we use the variable q' to make that distinction.

Now, replace the skin between stringers #7 and #1. Since the resultant shear force passes though the shear center, the twist angle must be zero. We use the angle of twist equation set to zero. This equation allows us to find the value of shear flow qo that once is algebraically added to q' values would give the true shear flow in each web.

This is the required shear flow to keep the closed section from twisting. Note that it is in terms of Vy.

By algebraically adding qo to q' in each web, we will come up with the actual shear flow distribution for the case when Vy is passing through the shear center

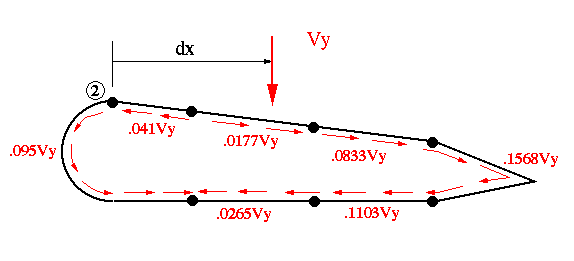
(b) To find the horizontal location of the shear center, we sum the moments about the position of one of the stringers. Here we choose stringer #2.

ex is measured from the centroid of the cross section.

(c)

To determine the shear flow distribution for V = Vx and Vy = 0, we pretty much follow the same procedure as used in part (a). Again, remove the skin between stringer #7 and #1. With Vy = 0, equation A14.14 reduces to

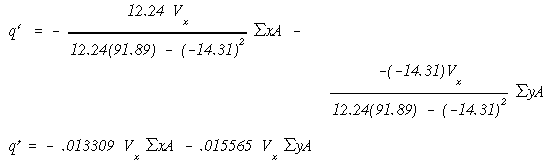
As before, work all the way around the section to find q' in each web.

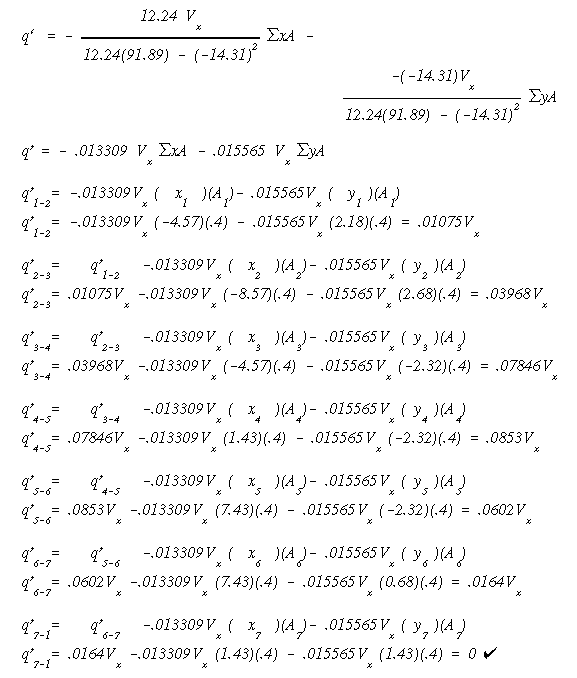
Use the angle of twist equation set to zero to solve for qo.

By algebraically adding qo to q' in each web, we will come up with the actual shear flow distribution for the case when Vx is passing through the shear center

Note the direction of shear flow around the section. To check the validity of the shear flows, we can sum forces along the x direction to make sure it comes out to be equal to Vx which is the resulant force of all shear flows.

Finally, we sum moments about the position of stringer #2 to solve for dy and ey.

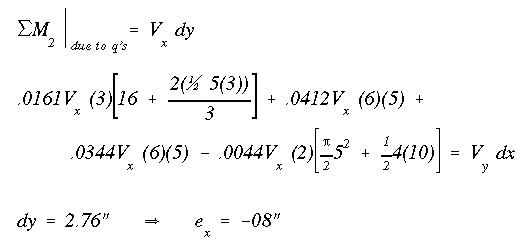
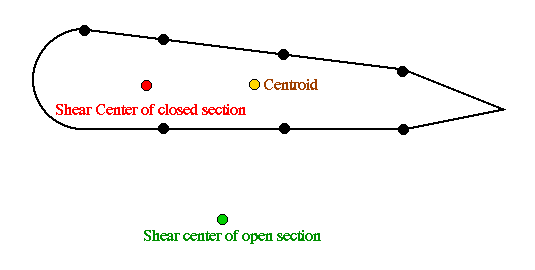
Therefore, the shear center is located at 5.85" to the left and .08" below the centroid as shown in the figure below.

Just for the curiosity sake, where would the shear center be if there really was no skin between stringers #7 and #1, making this an open skin-stringer section?

It can be easily found by using the q' values in the above analysis in the equation for the summation of moments. Use the q' in part (a) to find the ex and use the q' in part (c) to find ey in this case. The shear center would be located at

This location is consistent with the location of the shear center for a channel section.

To Section IV.3

To Index Page of Transverse Shear Loading of Closed Sections