Section A6.17 example 1

Section A6.17 example 1 SECTION A 6.17 EXAMPLE 1

A wing spar has a cross-sectional shape shown below. It is fixed at the root, i.e., x=0 and free at the tip, i.e., x=200 in. What is the percentage of torque due to bending to that of the total torque, at x=2", x=20", and x=200"? If T=1000 in-lb, what would the angle of twist be at each value of 'x'?

EQUATIONS USUED

SOLUTION

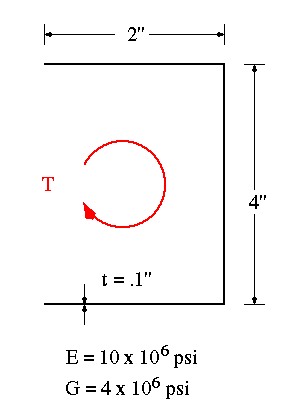
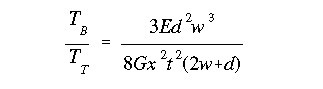
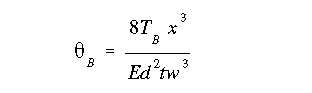
The equation for the ratio of TB to TT was derived earlier in the discussion. With the material properties and geometric parameters known, we calculate the torque ratio for different values of x as follows:

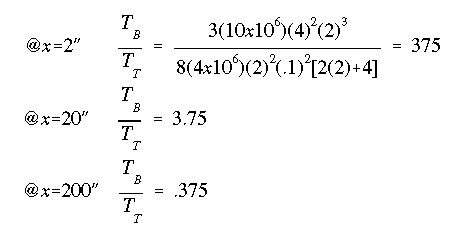
To find the percentages, it takes a little manipulation, but the results are:

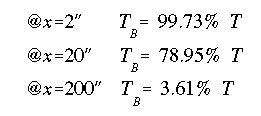
Notice the rapid decrease in the percentage of T carried in the form of differential bending of flanges as x increases.

The angle of twist at different spanwise stations is calculated by using the angle of twist equation with different values of x. Note that we can use either the angle of twist based on TT or TB, the result would be the same.

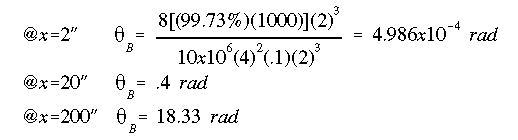
The angle of twist increases going from the fixed end to the free end.

This example is used to show that in the presence of an end restraint, the load in the bar is carried differently at the free and fix ends. It also shows how the load is carried in between the extreme points in the problem.

To Section A6.17

To Index Page of Pure Torsion