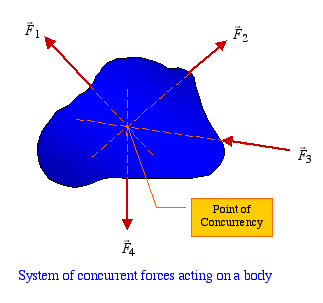
Equilibrium of a Particle: By particle we mean an object whose physical dimensions are of no significance to the analysis of forces acting on it. Hence, a particle is not necessarily a small object. All the forces in this case would pass through a single point resulting in a concurrent force system.

Since the forces acting on a particle always form a concurrent system, the equilibrium of forces gives the necessary and sufficient condition for equilibrium of the system. When we say a particle is in equilibrium, we mean that all the forces acting on it are in balance or that the resultant force is zero.
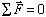 (1) (1) |
Equation (1) is a vector representation of force equilibrium. Realizing that each force vector acting on a particle could have up to three Cartesian components, and that for Eq. (1) to be satisfied all the individual components must also add up to zero, we can write the scalar equilibrium equations as
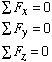 (2) (2) |
If all the forces acting on a particle are collinear, then the equation for force equilibrium in that direction is what we need to use. If, on the other hand, the forces are non-collinear, then we need to use two or three force equilibrium equations.
Free-Body Diagrams: Before we can apply the equilibrium equations, we must know exactly what forces are acting on a particle. We do this by drawing its free-body diagram. In this diagram, we show all the forces whether they are known or unknown. When we say a force is known, we mean its magnitude and direction are both known. As for an unknown force, we could have one of the following three conditions:
- Magnitude is unknown, but direction is known
- Magnitude is known, but direction is unknown
- Both magnitude and direction are unknown
When we are interested in analyzing forces in a particular section of the structure that can be modeled as a particle, we draw the free-body diagram of it by cutting (isolating) that section from the rest of the structure. We must be careful with showing the forces in members that have been cut. These forces typically have unknown magnitudes and sometimes even unknown directions.

If we know the line of action of a force vector but not its magnitude and sense, we show the unknown force with an assumed sense. We then formulate the equilibrium equations to solve for the unknown magnitude. If the magnitude is found to be positive, then the assumed sense is correct. Otherwise, the correct sense is opposite to that assumed.
If both magnitude and direction of a force are unknown, then we show the force in terms of its rectangular components. Similar to the previous case, we make an initial assumption on the sense of each component. With the help of equilibrium equations we solve for the magnitude of each component. If found positive, the assumed sense is correct.
When two bodies are in contact, and we want to draw the free-body diagram of one of them, we have to account for the force or forces at the point or surface of contact. If the surface of contact is frictionless (smooth), then the contact force is normal to the surface. If the surface is not smooth, then there is also a friction force tangent to the surface.