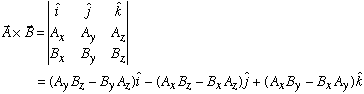Definitions and Laws of Vector Algebra:
1. A unit vector is defined as a vector whose magnitude is unity. If we divide a vector by its magnitude, we obtain a unit vector in the direction of the original vector. A unit vector can be expressed as
 (3) |
We can also express any vector in terms of its magnitude and the unit vector in the same direction as
|
|
(4)2. A vector may be represented in rectangular Cartesian coordinates as
|
|
(5)where 
are the unit vectors along x, y, z axes,
respectively.
3. The magnitude of a vector can be determined as
 (6) |
4. Two vectors are equal only if they have the same magnitude and direction. This condition can be described mathematically as follows:
Vector 
is equal to vector 
only when
5. When two or more vectors are added together, the resulting vector is called the resultant.
5.1 Commutative law for addition:
5.2 Associative law for addition:
6. If a vector is multiplied by a scalar as in 
, then the magnitude of the resulting vector is
equal to the product of p and the
magnitude of 
, and
its direction is the same as if p is
positive and opposite to if p is negative.
6.1 Associative law for scalar
multiplication: 
6.2 Distributive law for scalar
multiplication: 
7. A vector can be multiplied by another vector either through a dotor a crossproduct
7.1 Dot product of two vectors results in a scalar quantity as shown below
, 
where q is the angle between vectors and 
.
The dot product is performed as
In dot product, the order of the two vectors does not change the result.
7.2 Cross product of two vectors results in another vector quantity as shown below
, where 
and
q is the angle between vectors and . The direction of
vector 
is
perpendicular to the plane containing vectors and such that 
follow the right hand rule.
The cross product is performed as
In cross product, the order of vectors is important.  The associative law of multiplication also applies to cross product.
|
