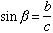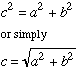Review of Plane Trigonometry: The parallelogram law is a powerful tool, but we don't want to rely on graphical measurements to determine the magnitude and direction of the vector resultant. What we would like to do is to use trigonometry instead. In this section, we will review the basics of trigonometry and the corresponding laws that are commonly used in Statics.
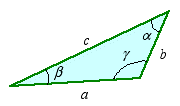
Law of Sines: For an arbitrary plane triangle of sides a, b, cand interior angles α, β, γ as shown below, the law of sines is expressed as
|
|
|
Law of Cosines: For the same arbitrary triangle of sides a, b, c and interior angles α, β, γ, the law of cosines is expressed as
|
If we know the lengths of two sides and the magnitude of the angle in between, then we can solve for the length of the third side using the above relationship.
Special Case of a Right Triangle: If one of the three angles (for instance g) is 90°, we will have a right triangle. In this case, Eq. (1) reduces to
|
|
We also have the following trigonometric relations for the right triangle
|
|
 For example, if the values of a, b and angle α or
β are known, then we can solve for side cand the other two angles using Eq. (1) and the fact that
For example, if the values of a, b and angle α or
β are known, then we can solve for side cand the other two angles using Eq. (1) and the fact that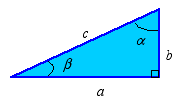
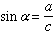 ;
;