Parallelogram Law: This is a graphical method used for a) addition of two vectors, b) subtraction of two vectors, and c) resolution of a vector into two components in arbitrary directions.
Vector Addition: Consider vectors 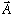 and
and 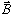 as shown
below. The addition of these two vectors gives the
resultantvector. The following steps are used to find the
resultant vector.
as shown
below. The addition of these two vectors gives the
resultantvector. The following steps are used to find the
resultant vector.
Step 1: As the first step, we draw
a line, at the head of vector 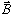 , parallel
to vector
, parallel
to vector 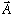 . We then repeat this for the
other vector.
. We then repeat this for the
other vector.
Step 2: Next, we draw a line from the point of concurrency of the two vectors to the point of intersection of the two parallel lines.
Step 3: Finally, we complete the parallelogram sketch with the diagonal representing the resultant vector.
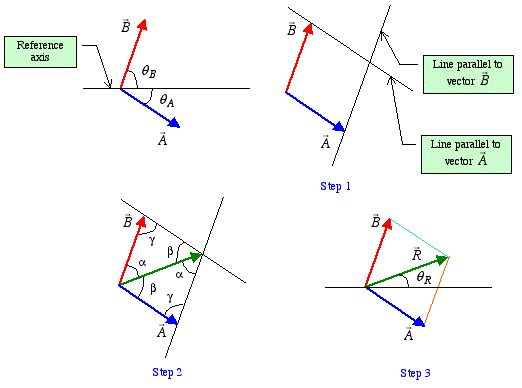
Notice that in constructing a parallelogram, the two vectors being added have to be shown in a tail-to-tail arrangement.
Vector Subtraction: If we are interested
in subtracting vector 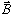 from vector
from vector 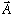 , we can represent this operation as the
addition of vectors
, we can represent this operation as the
addition of vectors 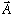 and (-
and (-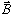 ). Notice that -
). Notice that -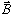 has
the same magnitude as
has
the same magnitude as 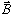 , but is in
opposite direction.
, but is in
opposite direction.
Step 1: As the first step, we flip
the direction of vector 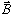 to create vector
-
to create vector
-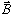 . Then slide it along its axis such that
vectors
. Then slide it along its axis such that
vectors 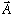 and -
and -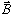 are tail-to-tail.
are tail-to-tail.
Step 2: We then repeat step 1 used in vector addition. We draw a line at the head of each vector parallel to the other vector.
Step 3: The parallelogram law is shown below with the diagonal representing the resultant vector.
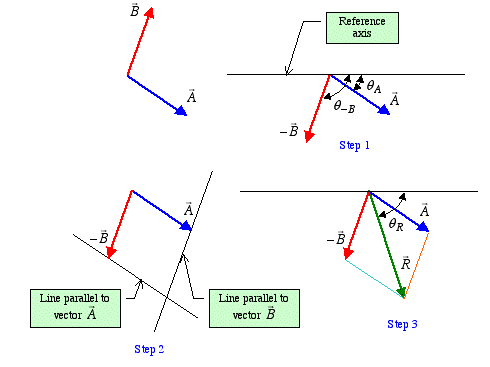
Resolution of a Vector into Two Components: We can also use the parallelogram law to determine the components of a vector along any two arbitrary axes. Click the mouse over each step to see the flash animation of this procedure. Also demonstrated is the head-to-tail construction of vector triangles.
Animation of Steps in Resolving a Vector into Two
Components
|