Equilibrium of a Rigid Body: A body is in the state of equilibrium if it is at rest or is moving at constant velocity. As there is no translational or rotational acceleration, the condition of equilibrium for a general three-dimensional system can be expressed as
|
|
(1) |
|
|
(2) |
Equation (1) simply states that the summation of all the forces acting on the body must be zero. To use this equation, all forces must first be expressed in Cartesian vector form. Similarly, Eq. (2) shows that the summation of all the moments must be zero. In this case also all the couple moments and moments due to individual forces must be expressed in Cartesian vector form.
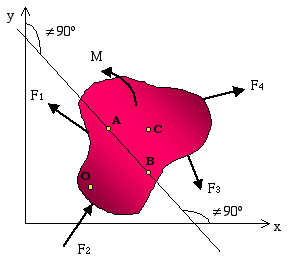
2-Dimensional Loading System: For a body under a two-dimensional loading system (e.g., in xy plane), the equations of equilibrium can be expressed in scalar form as
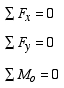 |
(3) |
Where point o represents an arbitrary moment center about which we determine the moments associated with each force. Notice that since all the forces are in xy plane, the equilibrium of forces in the z direction is excluded from this equation set. Furthermore, with all the forces being in the xy plane, they would only produce moments about the z axis, and that explains the exclusion of the other two moment equilibrium equations. Equation set (3) is the most common set of equations used for equilibrium of rigid bodies under a two-dimensional loading system. However, it is also possible to use alternative sets to Eqs. (3) given as
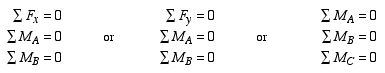 |
(4) |
When using the first set of equilibrium equations in (4), points A and B must be selected such that a line passing through them is not perpendicular to the x axis. Likewise, when using the second set, the line passing through points A and B must not be perpendicular to the y axis. For the last set, points A, B and C are three separate moment centers that do NOT fall on a straight line. Irrespective of which set we use, the results will be identical. Although in the last set only the equations of moment equilibrium are used, the equilibrium of forces will be met implicitly.
3-Dimensional Loading System: For a body under a three-dimensional loading system, the equilibrium equations i.e., Eqs. (1) and (2) in scalar form are given as
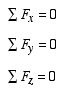 | (5) |
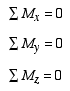 |
(6) |
The concept of equilibrium is without a doubt the most fundamental concept in statics. It enables us to determine the unknown forces and moments acting at joints, supports, surfaces of contact, etc.