Second Moments of Area

Parallel-Axis Theorem: 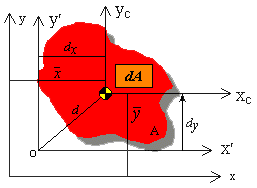In many instances the moment of inertia of an area about an axis that is parallel to its centroidal axis is sought. The equations for moments of inertia about such parallel axes are given as

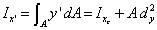	(5)
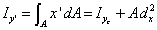	(6)

where I_xc and I_yc are the moments of inertia of the area about the centroidal axes x_c and y_c, respectively. d_y is the perpendicular distance between the centroidal axis x_c and the parallel axis denoted by x', while d_x is the perpendicular distance between y_c and y'. The x and y axes in this case serve as reference axes for finding the centroidal location of the area.

The parallel-axis theorem also applies to the polar moment of inertia

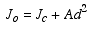(7)

where J_o is the polar moment of inertia about point o, J_c is the polar moment of inertia about the centroid, and d² = d_x² + d_y².

Similarly, the product of inertia with respect to x'y' axes can be found using the parallel-axis theorem as

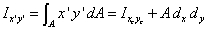(8)

 

The parallel-axis theorem is used in calculating the moments of inertia of a composite shape, one made up of a collection of elementary shapes. In that case, the moment of inertia of each elementary shape about its own centroidal axes are obtained first, then the corresponding parallel axis terms are added to determine the moments of inertia of the composite area. This procedure is demonstrated in the following example.

Example 5 (LiveMath)