Second Moments of Area

Product of Inertia: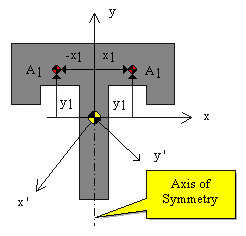The area product of inertia is defined as

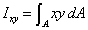(4)

The x and y terms inside the integral denote the centroidal position of the differential area measured from the y and x axes, respectively. Similar to moments of inertia discussed previously, the value of product of inertia depends on the position and orientation of selected axes. It is possible for the product of inertia to have a positive, negative, or even a zero value.

If, for example, either x or y represents an axis of symmetry, then the product of inertia I_xy would be zero. To see why this is the case, take a look at the figure to the right. Consider the small area A₁ to the right of y axis at the distance of x₁. Then consider a similar area to the left of this axis of symmetry at the distance of -x₁. Since both areas are at the same vertical position from the x-axis, they have the same value of y. The contribution from the left area is -x₁yA₁ and that from the right is x₁yA₁ which add up to zero. Since every point on one side of the axis of symmetry has an equal counterpart on the other side, the total value of the integral would be zero.

However, if we were to consider the product of inertia with respect to the x' and y' axes, then I_x'y' would not be zero. We will have more discussion about the product of inertia in the section on principal axes.

Example 4