Support Reactions:
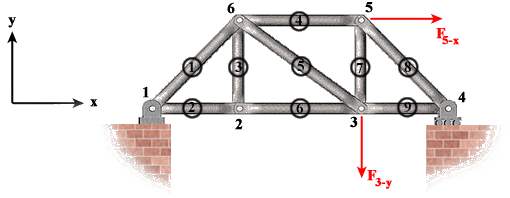To solve for the
support reactions the free-body diagram of the truss, as a unified
structure, is drawn first (move the mouse
over the figure to see the free-body diagram). This
free-body diagram shows the external shape of the truss with the
applied and reaction forces clearly identified. The reaction
forces, shown in green, are drawn in the positive x and y
directions. The correct direction of each reaction will be
determined from the equilibrium equations.
We begin the solution procedure by writing the moment equilibrium equation. Moments should be summed about a joint with the most reactions (i.e., unknowns). In this case, it would be wise to select joint 1 as the moment center and the origin of the coordinates xyz. Using the counter clockwise direction as positive, we obtain the following equation with one unknown (R4-y)
 |
 |
 |
|
 |
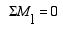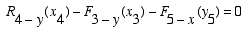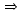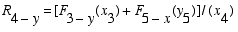We then write the force equilibrium equation in the x direction to solve for R1-x.
 |
|
 |
|
 |
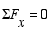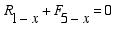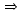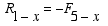Thus, R1-x is in the -x direction because of the negative sign in front of its magnitude.
Finally, we write the force equilibrium equation in the y direction to solve for R1-y.
 |
|
 |
|
 |
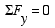
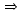
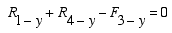