SECTION II.4 EXAMPLE 1
For the beam section and loading shown, determine

EQUATIONS USED

SOLUTION

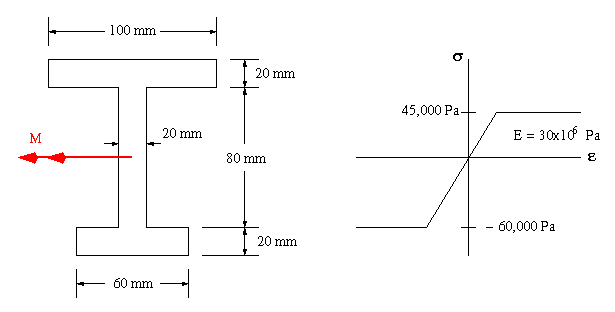
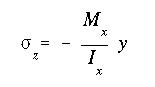
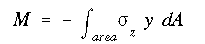
We must first find the location of centroid and the moment of inertia about the horizontal centroidal axis (x axis)

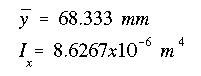
The moment of inertia about the x axis is all that is needed because with the product of inertia Ixy equal to zero and no moment about the y axis, the general elastic bending formula reduces to

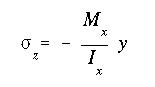
(a) Because the elastic-limit stress in the tension side of the stress-strain diagram is less than that in the compression side, the tensile limit will be the maximum stress allowable. Since the bottom side is in tension, let the stress at that location be equal to the limit of 45,000 Pa. This gives a maximum moment of

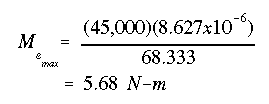
Now, check the top to make sure the compressive stress doesn't exceed its limit (60,000 Pa).

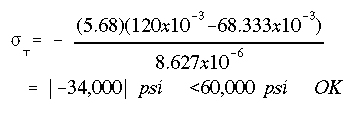
Therefore, the maximum elastic moment is

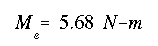
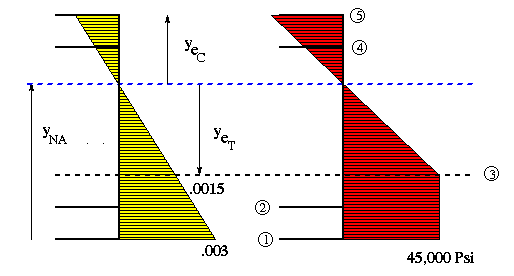
The strain and stress diagrams corresponding to the maximum elastic moment are shown below. Notice that the NA in this case coincides with the horizontal centroidal axis (x axis).

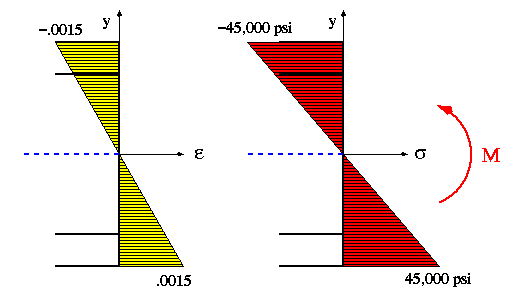
(b) We know the elastic-limit strain in tension and compression to be

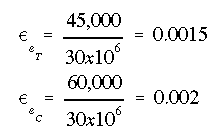
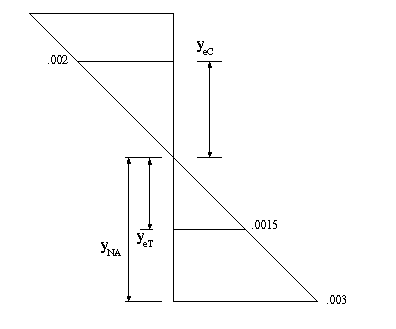
With the strain at the bottom now at 0.003, the elastic-inelastic interface, so to speak, is at some location between the NA and the bottom surface. Since stress-strain variations in tension and compression are different in the inelastic region, the NA will not pass through the centroid. Therefore, NA will not coincide with the x axis in this case. However, the NA will be parallel to the x axis. So we know its orientation but not its location. The location of NA is found through an iterative process.

Assume NA is @ 68.333 mm from the bottom. Through similar triangles, the elastic-inelastic interface can be found



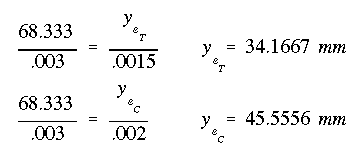
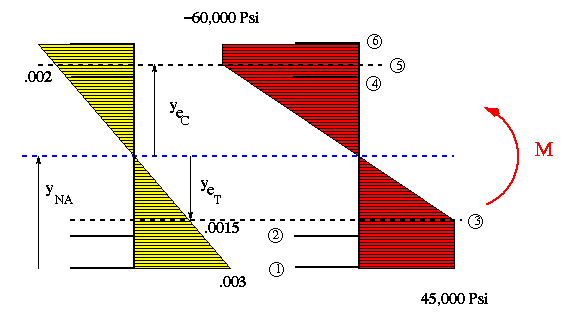
If the location of NA is correct, then the summation of forces in the normal direction must be zero.

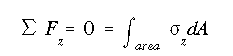
Based on the stress diagram shown above, the force equation is written as

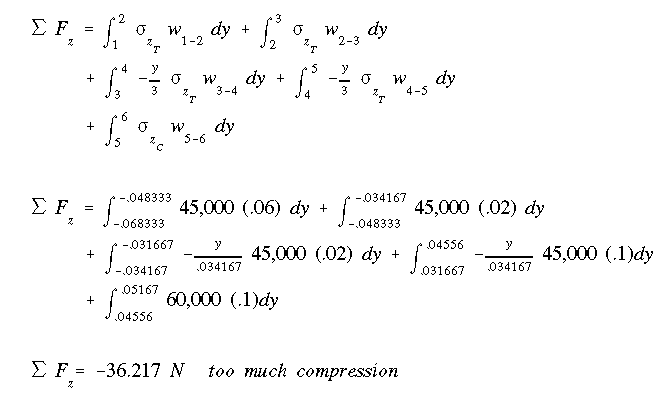
Since the sum of axial force components is not zero, the assumed location of NA is incorrect. The negative value indicates that the NA must be moved in the compression side as to reduce the area which is in compression or to increase the area in tension. For the second guess, assume NA to be @ 80 mm from the bottom surface and repeat the procedure.




The force sum is now positive indicating that the correct location of NA is somewhere between the two locations assumed previously. Using linear interpolation, we come up with the third guess

Using linear interpolation again and finding the summation of forces yields

The result is satisfactory. Now with the location of the NA known, the moment corresponding to the strain of 0.003 at the bottom side can be calculated.



(c) To find the fully-plastic moment, we must first determine the location of NA resulting in the total axial force to go to zero. In this case, there is no linear stress region. The compression and tension sides are under the state of constant stress equal to the corresponding maximum stress values.

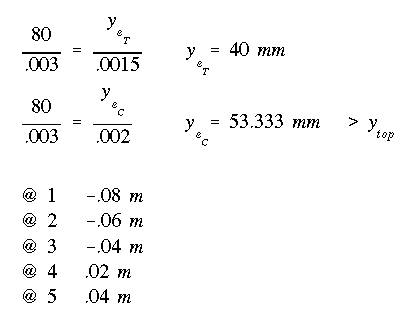
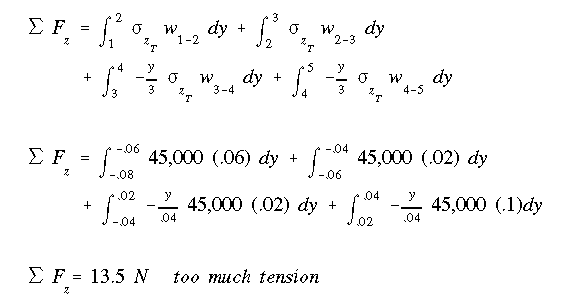
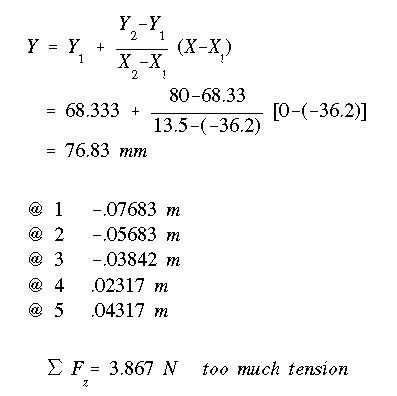
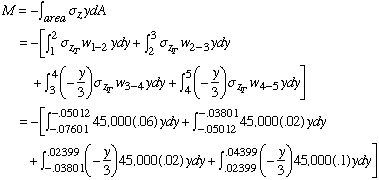
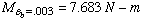
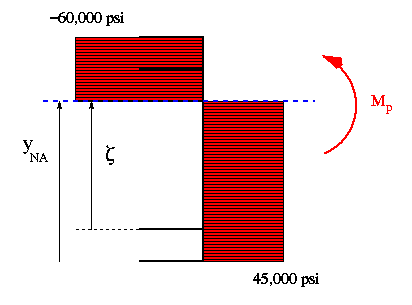
Using the stress variation shown above and the corresponding force summation, we find the location of NA as follows


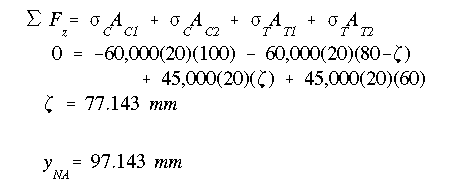
The fully-plastic moment is found to be

The results indicate that in this case the fully-plastic moment is 57% larger than the maximum elastic bending moment. We also saw in this problem that the location of neutral axis changed depending on the magnitude of M. The two factors having the most influence on the results are: (a) Different material elastic limits in tension and compression, and (b) Unsymmetric cross section with respect to the moment axis.
To Section II.4

To Index Page of Pure Bending