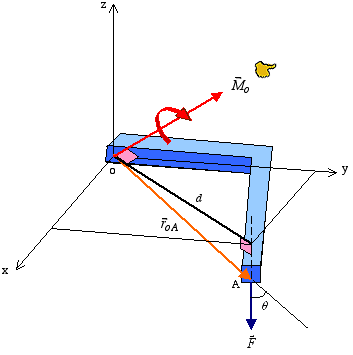
Vector Representation: The moment of a force about an arbitrary moment center "O" can also be described by the vector equation
 |
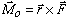(4) |
where 
is
the position vector measured from the moment center to any point
along the line of action of the force vector 
. The
directional sense of the moment is found by first aligning the
position and the force vectors tail to tail, then curling the
four fingers of the right hand from 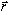to
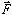with the thumb pointing in the direction of the
moment vector. The axis of the moment vector
passes through the moment center and is perpendicular to
the plane containing 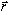and 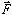. The magnitude of moment is measured
in units of force times length (e.g., lb·in or
N·m).
To calculate the moment of a force using the vector approach, we must know:
Force vector
Location of the moment center
Position vector (measured from the moment center to any point along the line of action of the force vector)
The following example describes the calculation of moment using the vector approach.
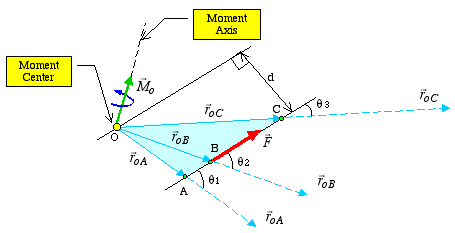
It is important to note that the position vector can be measured
from the moment center to any point along the line of action
of as
shown in the figure below. The resulting cross products in all cases will
be equal. That is
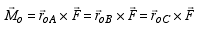
The reason all cross products in the above equation give the same answer is because
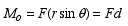
and
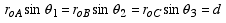
where θ is the angle between the
tails of
and .
|
Therefore, if we slide the force vector to any location along its line of action, its moment with respect to any arbitrary point or moment center will remain unchanged. This attribute is generally known as the principle of transmissibility. This fact is demonstrated in the following example. In the case of two or more forces, Eq. (4) is expanded to  (5) |
where N is the number of forces and 
represents
the position vector measured from the moment center to any point on
the line of action of 
. The following
example shows the calculation of moment due to multiple forces.