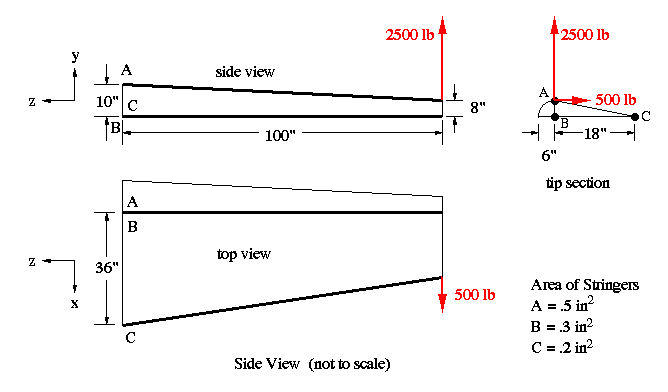
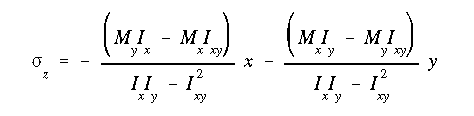
The centroid and the moments of inertia at station A-A are given below.
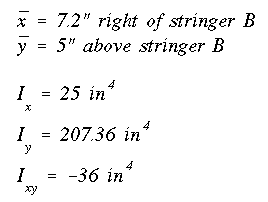
Use equation A13.13 to find the normal stress (i.e., that along the 'z' axis) for each stringer. Notice that the product of inertia is not zero since neither x nor y centroidal axis is an axis of symmetry.
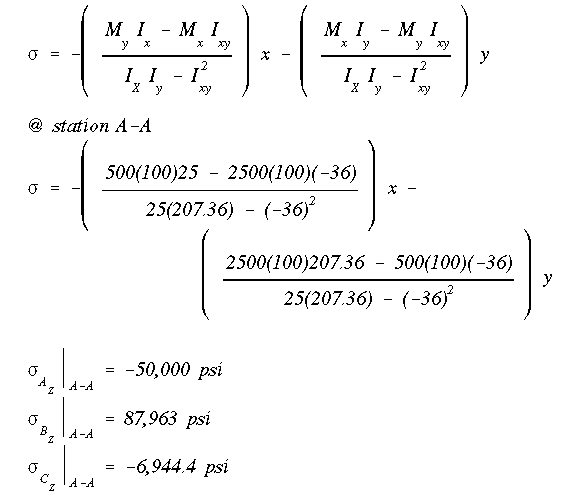
The z-component of each stringer force is just the stress times the area of each stringer.
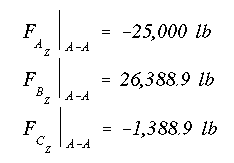
You should notice that these are the same values as found in Section IV.5 Example 1. Now repeat the procedure for B-B. Although the cross-sectional areas of stingers do not change, the moments of inertia and the centriod of the cross section do change because of taper in the webs. Therefore, they need to be calculated again. To start, we need to know the new coordinates of the stringers. This calculation is shown below for the stringer A. Stringer C is done in a similar manner.
The centriod location and moments of inertia are
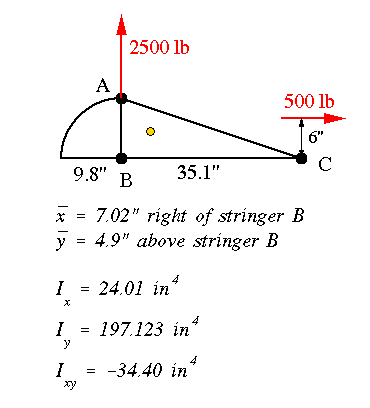
The stresses along the 'z' axis and the corresponding forces are:
The difference in the z-component of force at sections A and B gives the Delta p for each stringer. Because we are dealing with a box beam with tapered webs, the Delta p values are identified by subscript Z indicating the difference in z-component of the force in stringers.
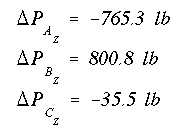
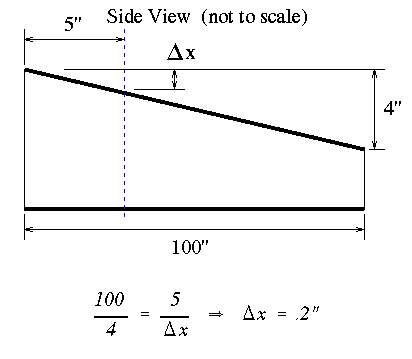
Now the Delta P along each stringer axis must be determined in order to do an accurate shear flow analysis. This can be done by using the geometric concept of similar triangles. For this cross section it will be easy because each stringer has a nonzero slope in only one plane as shown in the figure below.
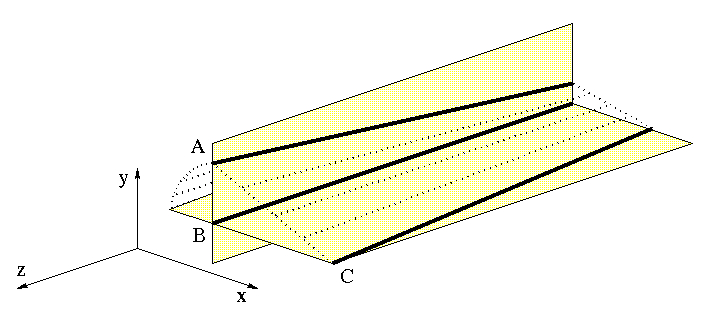
That is, stringer A in the 'y-z' plane and stinger B in the 'x-z' plane. If a stringer has nonzero slopes in two planes, the same approach can still be used.
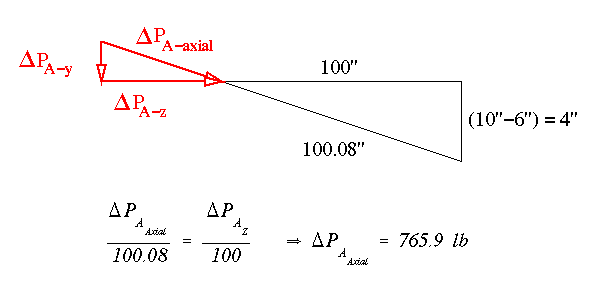
Starting with stringer A we have
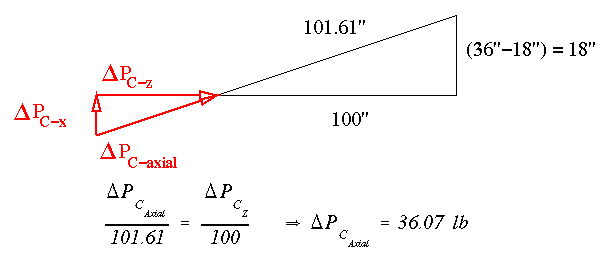
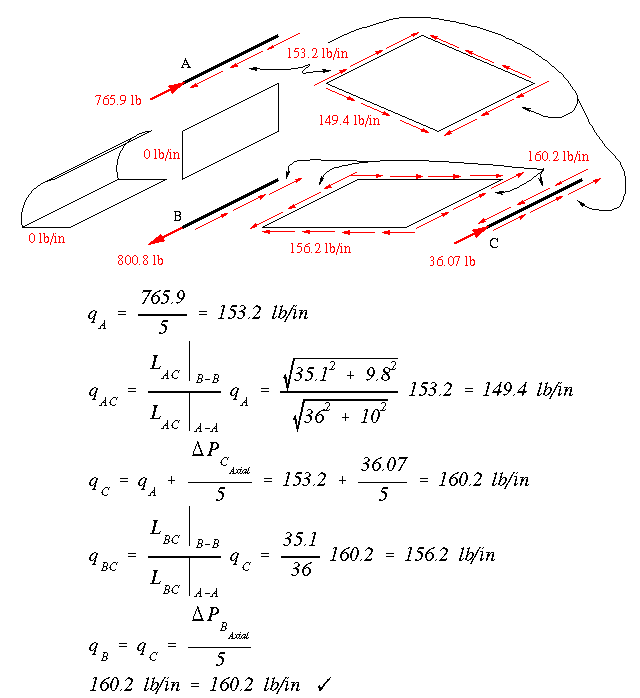
The Delta P for stringer B is the same as Delta Pz because the stringer is along the 'z' axis. At stringer C we have
Remove two webs to make this an open section. Webs AB (the quarter circle) and web AB (the interior flat web) are removed in this example. The shear flow for the cross section is calculated much in the same manner as in the last example. The difference is that the webs are tapered and although the shear flow is still constant along a particular side, the shear flows along two adjacent sides are not the same.
We start at stringer A and obtain the shear flow along its length.
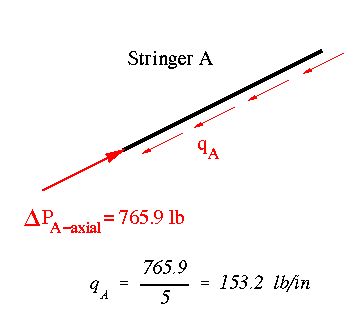
This shear flow is transferred to the top web
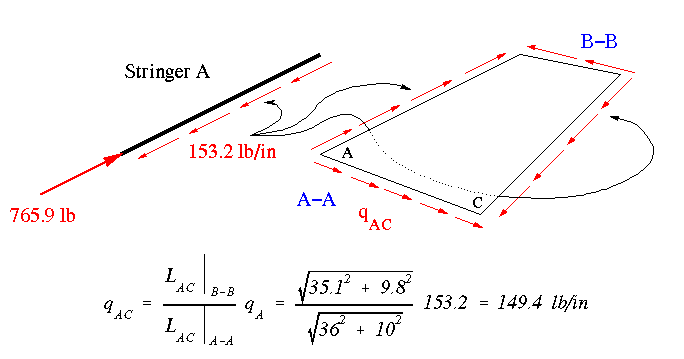
We calculate similarly the shear flow along the lower web at section B, and get
Now replace the two webs that we had removed, and use the angle of twist equation to obtain one equation in two unknowns (one for each cell). Note the 250 lb horizontal force at stringer C and the 1000 lb vertical force at stringer A at the root. These components are present because the axial forces in the stringers A and C are not normal to the plane of cross-sectional view. Therefore, they must be included in any moment summation.
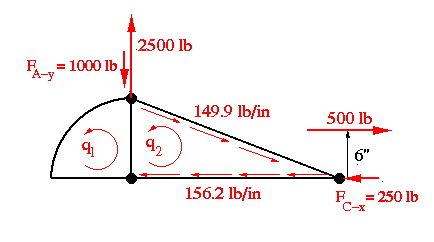
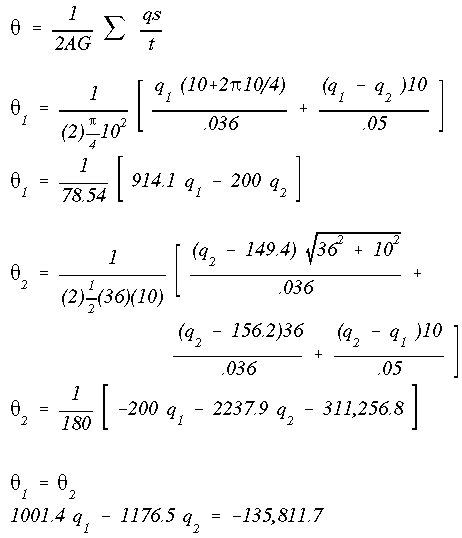
By summing the moments about 'A' we get another equation relating the two constant shear flows.
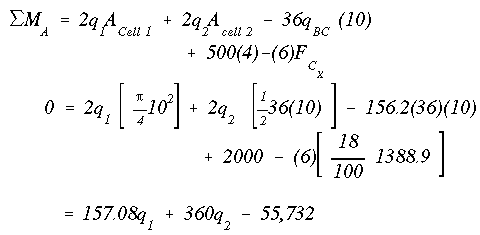
There are now two equations and two unknowns. Solving for the unknown shear flows gives
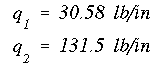
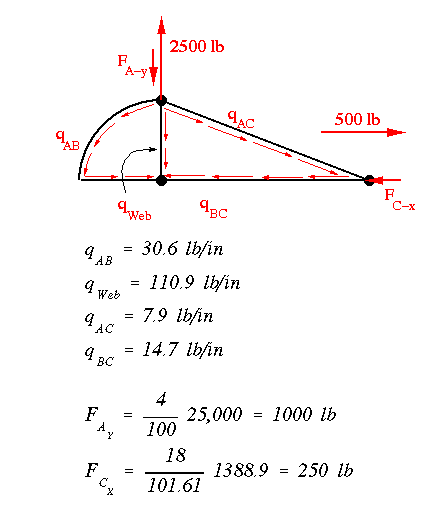
Just add up the respective shear flows (while paying attention to their directions) to obtain the final shear flow distribution at the root.
To Section IV.6
To Index Page of
Transverse Shear Loading of Closed Sections