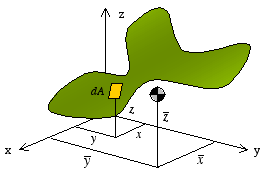
Centroid of Area

Centroid of Area: The centroid of an area of arbitrary shape, such as the one shown below, can be determined using the integral equations

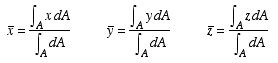(1)

where dA= differential area and x y z= moment arms of dA (identifying the coordinates of the centroid of dA, see figure)

Depending on the choice of differential area, we can have a single or a double integral in the numerator and denominator of each centroidal coordinate in Eq. (1) as demonstrated in the following examples.

Example 1

Example 2 (updated)

If the surface being considered has boundaries that allow it to be represented by a collection of simple shapes, then a modified version of Eq. (1) can be used. For such composite shapes, as shown in the figure below, we find the location of centroid as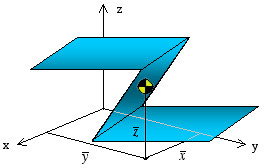

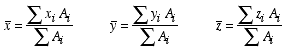(2)

where x_i, y_i, z_i denote the centroidal coordinates of the i^th element of the composite shape.

A composite shape should be subdivided in such a way as to simplify the calculation of centroidal location. In some cases it may be easier to think of the composite shape as a larger surface with a portion of it cut out. In the summation equation the area of the cutout portion would have a negative sign associated with it. The calculation of centroidal coordinates is demonstrated in the following example.

Example 3